Journal

This is going to be a very informal rolling journal about stuff I find interesting, my thoughts, notes, and anything of the sort. By no means should this serve as a comprehensive resource for any mathematical ideas. In that same vein, I am very aware that there exists mistakes and there will continue to be mistakes made. I'm not going to go back and edit any mistakes. This is a personal archive above all else so I am not terribly concerned with formalism. Always do your own research on anything I discuss here. However, I hope this inspires at least one of you to learn something new. Thats one of the beautiful things about mathematics, there is ALWAYS something more to learn.

September 24th - Clutching Functions and the Möbius Band

Yes it's been a hot minute but after settling in to my new home and PhD. program I'm finally ready to write some more. I want to talk about something pretty fundamental in K-theory and geometry as whole. Clutching functions are defined quite abstractly but hopefully I can demystify them a little bit. Consider a vector bundle $\rho:E \to X$ and an automorphism $f: E \times S^1 \to E \times S^1$. For each $x \in X$ and $z \in S^1$, $f$ gives an isomorphism $f(x,z): \rho^{-1}(x) \to \rho^{-1}(x)$. From $E$ and $f$, make a vector bundle over $X \times S^2$ by taking two copies of $E \times D^2$ and identifying the subspaces $E \times S^1$ via $f$. This results in a new bundle denoted $[E,f]$. Here, $f$ is the clutching function. Ok yes, this is a lot of algebra and probably doesn't make much sense. This is fine because I was completely lost until I boiled it down to a simpler example (this is 99% of mathematics lol).

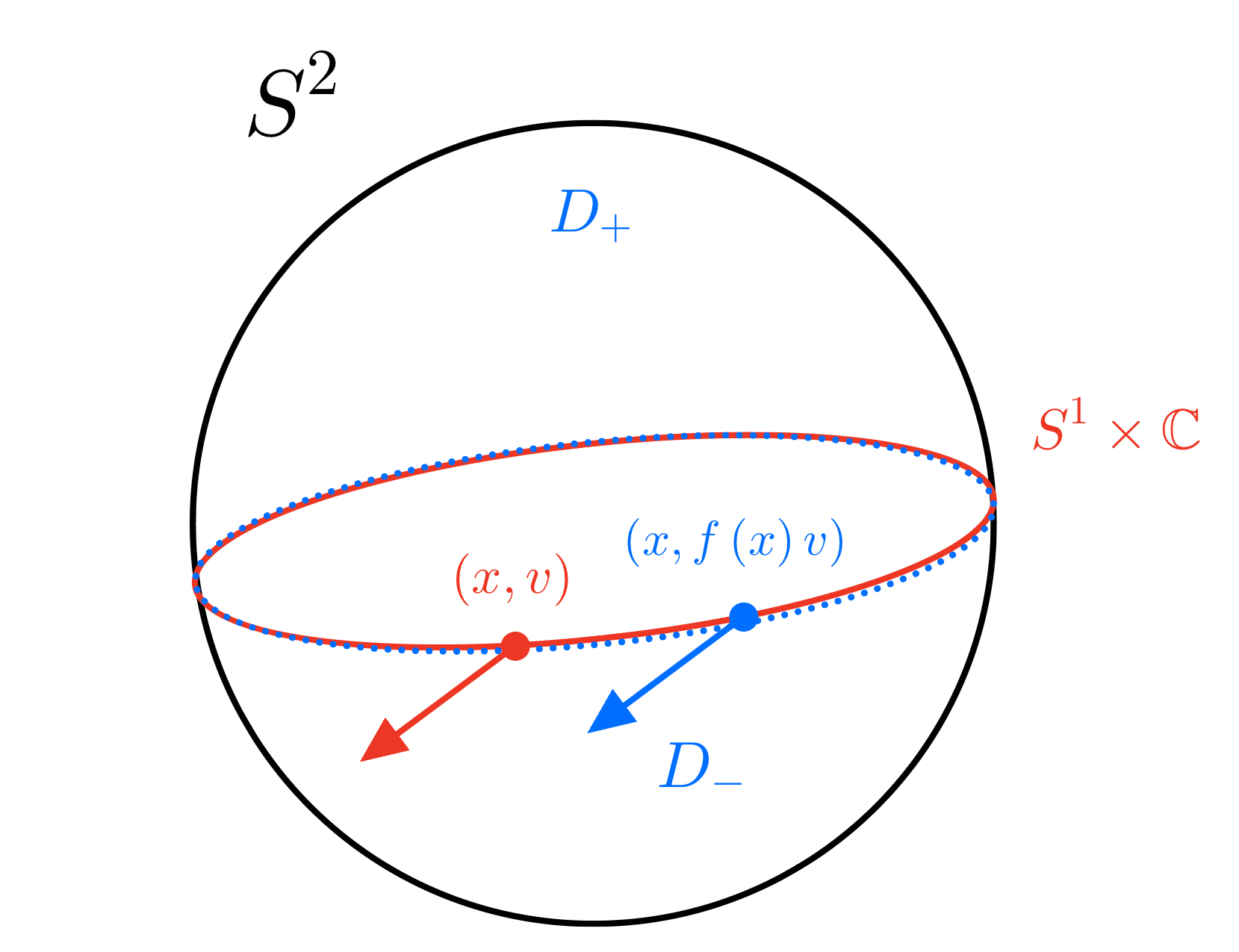
So lets consider a simple example on $S^2$. Let $D_+$ and $D_-$ be the upper and lower hemispheres respectively. It's clear that $D_+ \cup D_- = S^2$ and $D_+ \cap D_- = S^1$. So on the equator, we see we have two copies of $S^1$, one copy coming from $D_+$ and the other coming from $D_-$. The choice of clutching function will tell us how to glue these copies of $S^1$ together. If we take $f = \operatorname{id}_{S^1}$, we just get the regular equator and nothing changes. So we get something like $$ (x,v) \in S^1 \times \mathbb{C} \mapsto (x, f(x)v) \in S^1 \times \mathbb{C} $$

So we see the vector doesn't change relative direction as we slide it along $S^1$. Thus $f:S^1 \to GL_1(\mathbb{C}) = \mathbb{C}^\times$.

$f$ says how the fiber $v$ changes as we move along $D_+ \cap D_- = S^1$

If we took $f$ to be something other than the identity, the blue arrow would point in a different direction as we moved along the equator. This is in fact exactly what happens with the Möbius band.

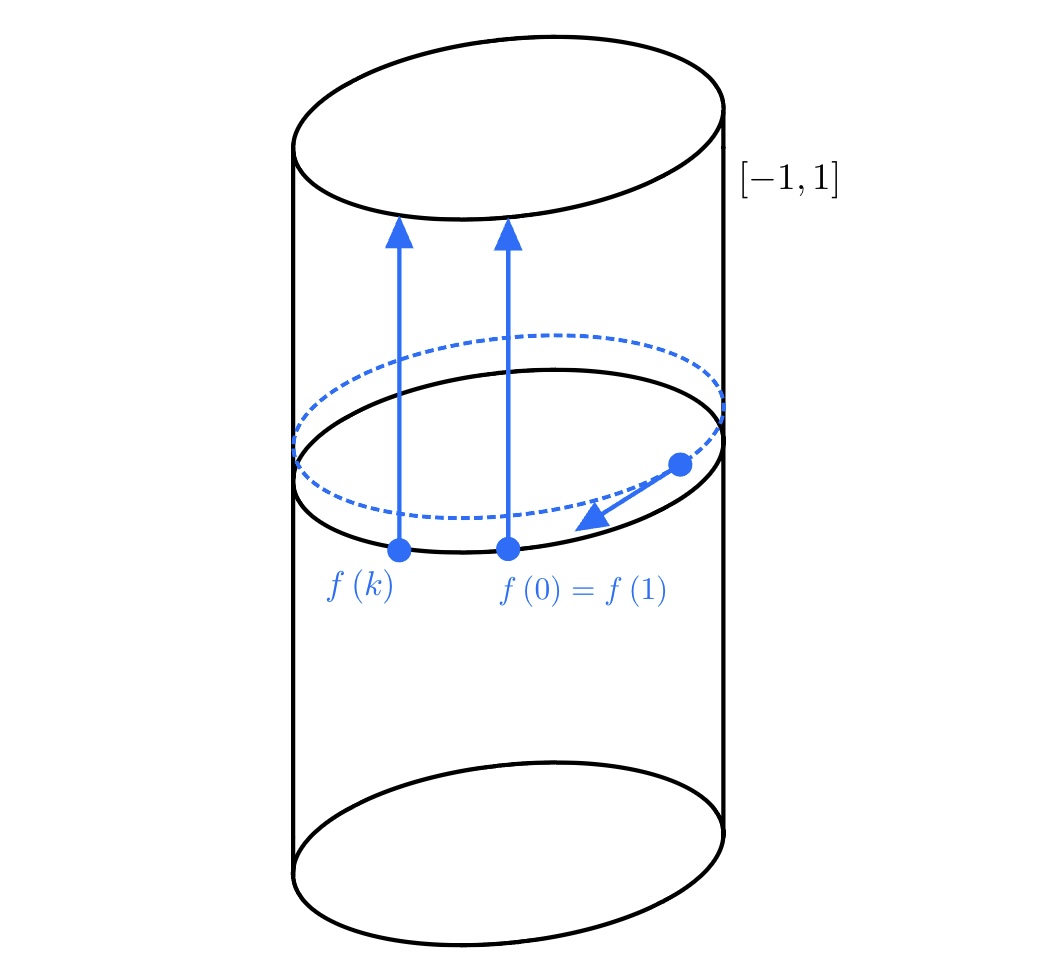
Choose the base space $E = \left( [0,1] \times [-1,1] \right) / \sim$ and choose the clutching function $f:S^0 \to GL_1 (\mathbb{R})$ such that $f(0)=1$ and $f(1)=1$. This trivial clutching function just gives us a cylinder of height $|[-1,1]|=2$. This is not particularly interesting, but if we change the endpoint of clutching function so that $f(1) = -1$, we get the Möbius band of width $2$. This is because as we move along $S^1$, a vector $v$ will reverse it's orientation after one complete lap around $S^1$. Once again, lets look at some pictures. First, the cylinder example.

So at the point $0$ on the circle, we see the vector $f(0)$ is pointing upward. As we continuously apply $f$ to points on the circle, the vector $f(k)$ always points upward. So this is the trivial clutching function. The vector $f(k)$ doesn't rotate or twist in any way as we walk around the circle. Now for my overly complex Möbius band. We start with the base point $f(0)=1$, this corresponds to the blue vector pointing straight upwards.

As we work around the circle (in the clockwise direction), we see that $f$ starts to twist the vectors (the "direction" in which they twist is not relevant for now, but this has to do with the idea of orientation). By the time we make our way around the whole circle, at $f(1)$, we see that the vector has been flipped upside down. This corresponds to $f(1)=-1$. This is the Möbius band. Here, I represented the width by the small black ticks but this is usually drawn with the width of $[-1,1]$. With enough squinting and a big enough imagination, I hope you can convince yourself this is in fact the Möbius band we all know and love. Lets also look at a more elegant drawing with the same identifications above in hopes of painting a clearer picture of the clutching function's role.

So think about how if I slide the red vector along the band in the counter-clockwise, the orientation will get flipped and it will lineup with the blue vector. Technically, $0 \sim 1$ on $S^1$ because we have to glue the endpoints with the reverse orientation. The clutching function $f=-1$ causes this flip. I didn't label it but the height of the band here is the interval $[-1,1]$, this is the usual choice when drawing the Möbius band, but in reality, we take the bundle over $S^1\times \mathbb{R}$ when describing the Möbius band analytically.

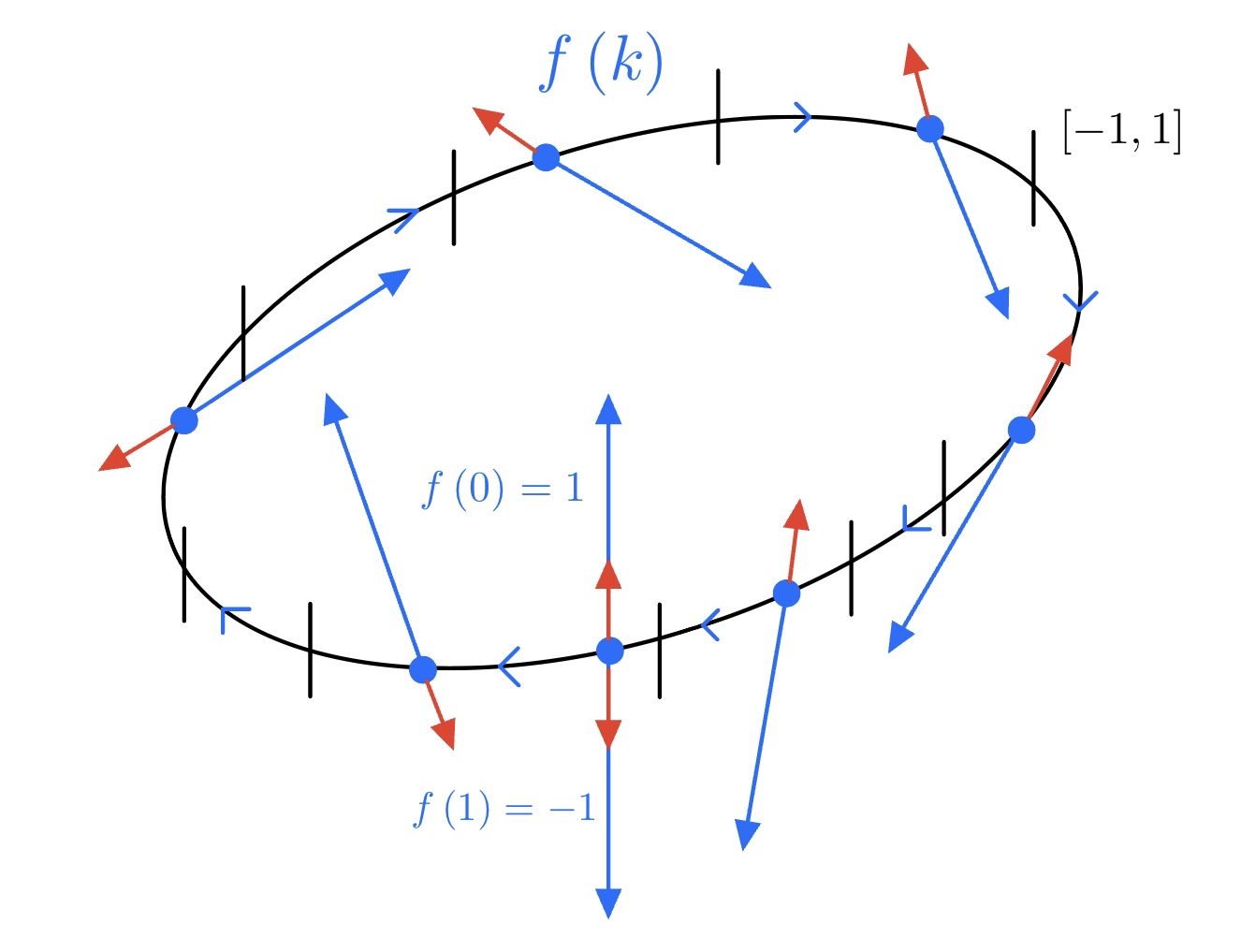
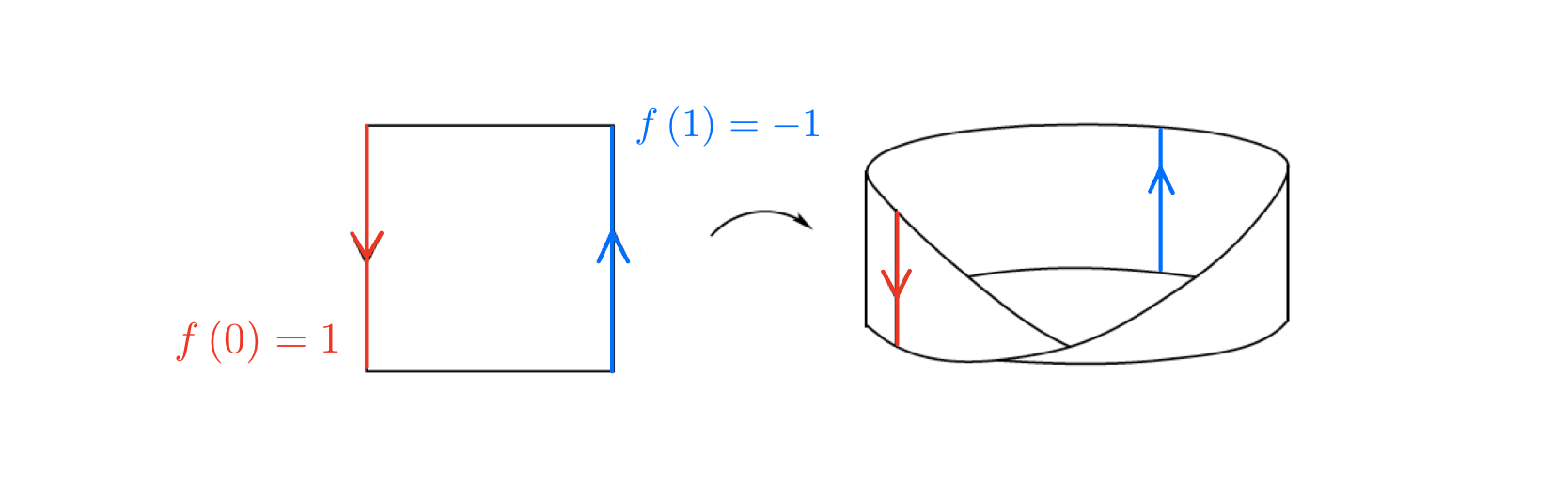
To quickly recap, we talked about the rigorous defintion of a clutching function and how it gives us a rule on how to glue fibers of vector bundles. We looked at the $S^2$ example with the trivial clutching function then the $S^1$ example with the inversion clutching function. Have some food for thought, what would happen if we used the inversion clutching function or something like $f(x)=x^k$ for the $S^2$ example?